Ultrafast Dispersion
This is Sections 12.1 and 12.2 of the Laser Optics Resource Guide.
While the effect of dispersion is minimal for many types of laser systems, it is especially problematic in ultrafast laser applications. Ultrafast lasers are characterized by short pulse durations on the order of picoseconds, femtoseconds, or attoseconds. Due to the Heisenberg uncertainty principle, transform-limited ultrafast pulses reaching the lower limit of their pulse duration have a wide wavelength bandwidth (Figure 1). As these wide bandwidth pulses transmit through optical media, chromatic dispersion lengthens the pulse duration, which is detrimental in ultrafast applications.
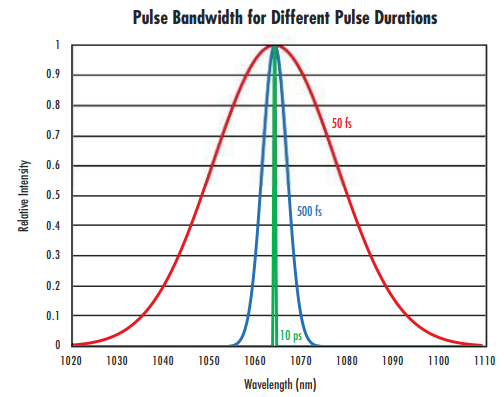
Figure 1: As the pulse duration of an ultrafast laser decreases, the wavelength bandwidth increases
Overview of Chromatic Dispersion
The way in which a laser pulse travels through an optical medium is described by group velocity $ \small{v_g}$ - the variation of the phase velocity of light in a medium relative to its wavenumber $ \small{k}$:
(1)$$ v_g = \left( \frac{\partial k}{\partial \omega} \right)^{-1} = c \left[ \frac{\partial}{\partial \omega} \left( \omega n \! \left( \omega \right) \right) \right] ^{-1} = \frac{c}{n \! \left( \omega \right) + \omega \frac{\partial n}{\partial \omega}} = \frac{c}{n_g \! \left( \omega \right)} $$
$ \small{\omega}$ is the light’s angular frequency, $ \small{c} $ is the speed of light in a vacuum, and $ \small{n} $ is the refractive index of the medium. The wavenumber $ \small{k}$ is $ \tfrac{2 \pi}{\lambda}$ - this concept is sometimes referred to as the spatial frequency of the wave. The difference between phase velocity and group velocity is illustrated in Figure 2.
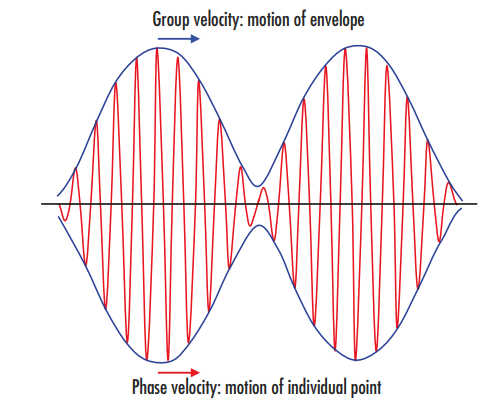
Figure 2: The group velocity defines the motion of the envelope, or wave packet, highlighted in blue, while the phase velocity defines the higher frequency motion of each individual point of the wave itself, highlighted in red
When light of multiple wavelengths travels through a material, it is common for the longer wavelength (low frequencies) to travel slightly faster than the shorter wavelengths due to a frequency (or wavelength) dependence of the group velocity.1 This causes a spectral variation of the phase of the wavefront in the same way that light traveling through a prism is broken into its component colors from spectral dispersion of the material. As the group velocity is given as the first derivative of phase velocity with respect to frequency, the group velocity dispersion $ \small{\left( \text{GVD} \right)} $ is the derivative of the inverse group velocity with respect to frequency:
(2)$$ \text{GVD} = \frac{\partial}{\partial \omega} \left( \frac{1}{v_g} \right) = \frac{\partial}{\partial \omega} \left( \frac{\partial k}{ \partial \omega} \right) = \frac{\partial ^2 k}{\partial \omega ^2} $$
The inverse group velocity is known as first-order dispersion, and $ \small{ \text{GVD}} $ is known as second-order dispersion. Just as the group velocity is similar to spectral dispersion, in that both correspond to the first derivative of refractive index with wavelength or frequency, the $ \small{ \text{GVD}} $ is used similarly to the partial dispersion as they are both second derivatives with respect to wavelength or frequency. Designing optics for low-$ \small{ \text{GVD}} $ is similar to designing for good chromatic performance, except the focus is placed on group velocity and $ \small{ \text{GVD}} $ rather than the related Abbe number and partial dispersion.
$ \small{ \text{GVD}} $ is independent of the length of the given optical medium. Group delay dispersion $ \small{ \text{GDD}} $ considers the length of the medium and can be found by multiplying the $ \small{ \text{GVD}} $ by the length.
(3)$$ \text{GDD} = \text{GVD} \times \text{Length} $$
$ \small{ \text{GVD}} $ is highly wavelength dependent and has typical units of $ \tfrac{\text{fs}^2}{\text{mm}} $. For example, the $ \small{ \text{GVD}} $ of fused silica is $ \small{+} 57 \tfrac{\text{fs}^2}{\text{mm}} $ at 589.3nm and $ \small{−} 26 \tfrac{\text{fs}^2}{\text{mm}} $ at 1500nm. Somewhere between those wavelengths (at about 1.3μm), there is a zero-dispersion wavelength where $ \small{ \text{GVD}} $ is zero. Figure 3 shows the significant amount of variation of the $ \small{ \text{GVD}} $ of fused silica vs. wavelength. For optical fiber communications, the $ \small{ \text{GVD}} $ is typically defined as the derivative with respect to wavelength instead of frequency and is usually specified with units of $ \tfrac{\text{ps}}{\text{nm km}} $.
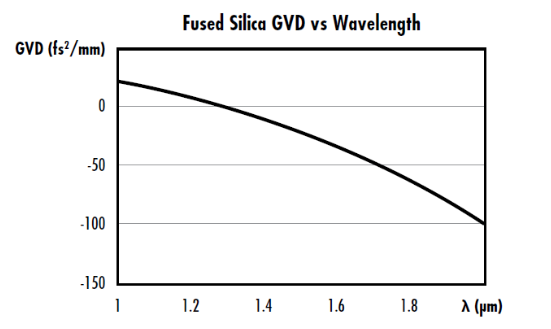
Figure 3: GVD vs wavelength for fused silica with a zero-dispersion wavelength around 1.3μm
Ultrafast Lasers
Ultrafast lasers are highly advantageous because of their short pulse durations and high peak powers for a variety of applications including precise biomedical applications, materials processing, micromachining, nonlinear microscopy and imaging, and communications. Ultrafast lasers lead to better dimensional tolerances in materials processing and micromachining while eliminating typical post-processing steps and minimizing damage to surrounding areas.2 Similarly, ultrafast lasers result in less trauma in laser surgery and other medical applications, while also lessening the need for anesthetics and sterilization.3 Ultrashort laser pulses are created when light waves containing a large quantity of modes, or integer multiples of half of the wavelength of the light, are emitted coherently through their in-phase superposition (Figure 4). This is also known as mode-locking.
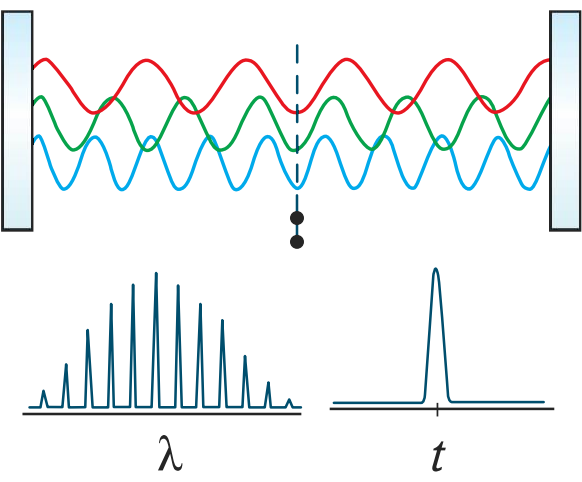
Figure 4: Interference of coherent waves with many modes during mode-locking generates pulses with an ultrashort temporal width but broad wavelength bandwidth
The dependence of $ \small{ \text{GVD}} $ on wavelength significantly affects ultrafast pulses due to their broad bandwidth, stretching out the pulse duration of ultrafast pulses as they travel through an optical system (Figure 5). The amount of pulse broadening from the incident pulse duration $ \small{\tau_{\tiny{\text{In}}}} $ to the output pulse duration $ \small{\tau_{\tiny{\text{Out}}}} $ is related to the $ \small{ \text{GDD}} $ (Figure 6):
(4)$$ \tau_{\tiny{\text{Out}}}= \tau_{\tiny{\text{In}}} \sqrt{1 + \left( \frac{4 \ln{\left( 2\right) \times \text{GDD} } }{\tau_{\tiny{\text{In}}} ^2} \right)^2} $$

Figure 5: Dispersion leads to the broadening of ultrafast laser pulses. AOM stands for acousto-optic modulator, which is a component that allows lasers to emit a pulsed output
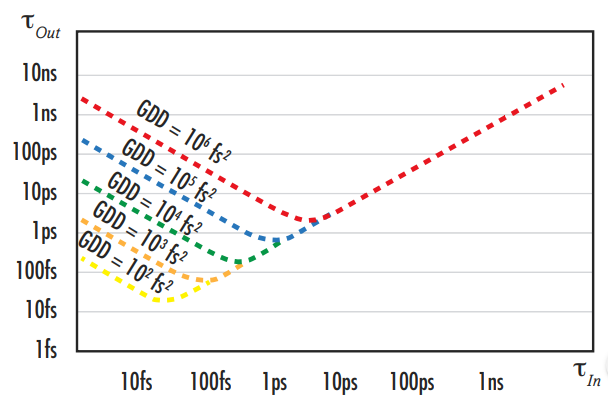
Figure 6: Depiction of temporal broadening, or increasing pulse duration, of a femtosecond ultrafast pulse after traveling through different optical media
Most optical media exhibit positive dispersion, so long wavelengths transmitting through them will have a higher phase velocity than that of shorter wavelengths, elongating the pulse duration (Figure 5). This is known as positive chirp. Ultrafast lasers are affected by dispersion significantly more than other laser types due to their broad bandwidth.
White light interferometry is the most common metrology used for measuring group delay and $ \small{ \text{GVD}} $ for ultrafast optical components. More information can be found in our Metrology for Laser Optics application note.
In addition to pulse broadening, chromatic dispersion may also make refraction angles at optical surfaces frequency-dependent, causing angular dispersion and frequency-dependent path lengths. Methods for dispersion compensation to improve the performance of ultrafast laser systems can be found in our Highly-Dispersive Mirrors application note.
ON DEMAND WEBINAR
Challenges and Solutions
Ultrafast lasers have revolutionized a number of application spaces, but optical components for these systems face a unique set of challenges that must be overcome to maintain high pulse quality and maximize performance.
- Ghatak, Ajoy, and K. Thyagarajan. “Optical Waveguides and Fibers.” University of Connecticut, 2000.
- Mielke, Michael. “Ultrafast Lasers: Ultrashort Pulse Lasers Bring Cost-Efficient Precision to Micromanufacturing.” Laser Focus World, 8 Apr. 2015.
- “The Benefits of Femtosecond Lasers and Why We Use Them.” Spindel Eye Associates, 16 May 2017, www.spindeleye.com/blog/2017/05/the-benefits-of-femtosecond-lasers-and-why-we-use-them/.
More Resources
- Highly-Dispersive Mirrors Application Note
- Highly-Dispersive Ultrafast Mirrors for Dispersion Compensation Video
- Ultrafast Lasers – The Basic Principles of Ultrafast Coherence Application Note
- LIDT for Ultrafast Lasers Application Note
- Trending in Optics: Reflective Laser Beam Shaping
- Trending in Optics: Ultrafast Highly-Dispersive Mirrors
- Laser Optics Lab Video Series













 Previous Section
Previous Section 































or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
California Consumer Privacy Acts (CCPA): Do Not Sell or Share My Personal Information
California Transparency in Supply Chains Act