Ultrafast Lasers – The Basic Principles of Ultrafast Coherence

The concept of atoms was coined by the ancient Greek philosophers Leucippus and Democritus twenty-four centuries ago.¹ However, it wasn’t until the late 20th century that atoms could be observed in motion and manipulated.² The temporal resolution required to manipulate atomic-scale dynamics with typical speed, on the order of 10 km/s, over a distance of 1Å, is 10 femtoseconds (10×10^-15 s). Hence, the visualization and manipulation of atoms and molecules requires laser pulses with durations on the order of the nuclear motion. Rapid advances in laser technology made it possible to produce pulses ranging between a few femtoseconds to tens of attoseconds (10×10^-18 s). Such pulses enable the direct investigation and manipulation of atoms and electrons, and extends the frontiers of science and technology to territories never thought accessible.

Lasers operate on two general principles: light amplification using a gain medium (e.g. Ti:sapphire crystal) and feedback ensured by a cavity (e.g. two mirrors). As light is amplified in the excited gain medium, an intense laser beam is produced due to the feedback of the cavity, which is partially transmitting (Figure 1).

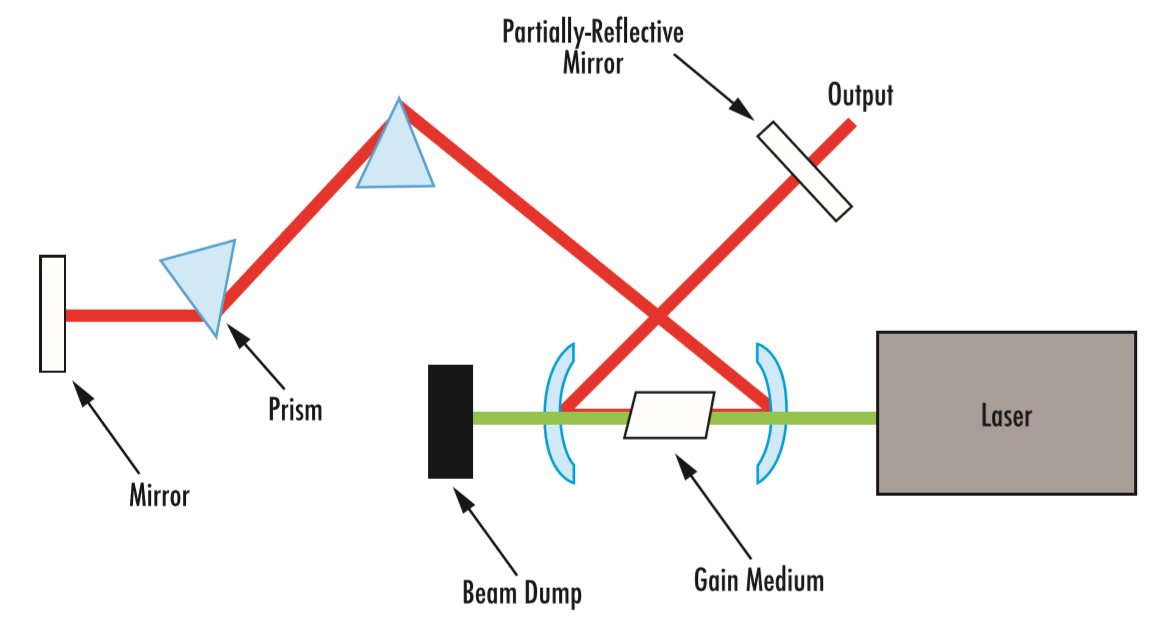
Figure 1: Typical optical setup of an ultrafast laser oscillator using a continuous wave (CW), second-harmonic generation, Nd:YAG laser

Ultrashort pulses are generated when light waves with a large number of modes, or integer multiples of half the light’s wavelength (λ), are coherently emitted through their in-phase superposition, also known as mode-locking. The broad energy bandwidth of ultrashort pulses is due to the uncertainty principle that arises from the inherent wave properties of photons where the precision of time-energy is limited by the Fourier transform. Since the energy (E=hc/λ) of ultrashort pulses can span multiple octaves in bandwidth, the crucial question that arises is whether such broad pulses retain coherency. The concept of coherence is extremely important in light-matter interactions at the ultrafast scale, to ensure interference effects between light waves and atoms/electrons populations. Such interference can be constructive or destructive depending on the phase difference between them (Figure 2).³

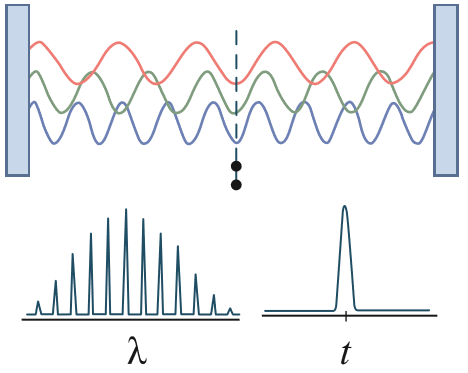
Figure 2: Basic concept of ultrashort pulse generation through mode-locking, resulting in pulses that have a broad wavelength bandwidth but ultrashort temporal width

Considering a Gaussian ultrafast laser pulse transitioning a system from one state χ₀ with energy E'₀ to other states φ_n with corresponding energies E_n, the wave function is given by:

(1)$$ \phi = \sum{a_n \varphi_n} $$

where α_n are the amplitudes of the eigenstates φ_n whose moduli squared represent the population probabilities of the individual eigenstates after the pulse is applied. From the first-order perturbation theory, these eigenstates can be determined as:

(2)$$ a_n = C \langle \varphi_n | \chi_0 \rangle \int^{+ \infty}_{- \infty} \exp{\left[ - \frac{i \left( E_n - E_0 \right) t }{\hslash} \right]} \cdot \exp{\left( \frac{-t^2}{\alpha \tau^2} \right)} \cdot \cos{\left( \omega t \right)} \, \text{d} t $$

where C is a constant dependent on the field amplitude of the pulse and the transition dipole moment and α = 2π²/ ln⁡(2). < φ_n | χ₀> is the Franck-Condon factor given by the integral between the initial and final states. The evaluation of the integral in Equation 2 yields:

(3)$$ a_n = C \langle \varphi_n | \chi_0 \rangle \cdot \exp{\left[ \frac{- \left( \omega_n - \omega \right)^2 \alpha \tau^2}{4} \right]} $$

where ω_n= (E_n- E'₀) / ℏ is the Bohr frequency. In the limit of an ultrashort pulse, the lifetime (τ) of the process under laser excitation approaches zero and α_n⁡= C < φ_n | χ₀>. Hence, ψ = C <φ_n | χ₀> φ_n= χ₀. Accordingly, the excited wave packet ψ possessing the same shape as the initial wave function, is a “coherent” superposition of excited eigenstates.

Based on this formalism, the coherent nature of ultrafast pulses offers a powerful technique for the control of multilevel atoms⁵, molecules⁶, semi-conductor spin states⁷, phase transitions⁸, and magnetism⁹ leading to applications not previously possible with other technologies. Using ultrafast lasers, structure-functionality paradigms in novel materials can be better understood, leading to the design of optimized functional materials through the dynamical manipulation of atoms, molecules, and monolayers.^10,11 The ability to accurately probe and control atomic and electronic dynamics has led to novel arrays of technological advancements based on ultra-precise measurement techniques and highly functional materials.

References:

B. Pullman, (1998). The Atom in the History of Human Thought. Oxford, England: Oxford University Press.
H. C. von Baeyer, Taming the Atom; Random House: New York, 1992.
A. H. Zewail, J. M. Thomas, 4D Electron Microscopy. Imaging in Space and Time; Imperial College Press, 2010.
T. E. Karam, Ultrafast and Nonlinear Spectroscopy of Colloidal Nanomaterials. (2016).
M.C. Stowe, A. Pe’er, J. Ye, Phys. Rev. Lett. 100, 203001 (2008).
M. Viteau, A. Chotia, M. Allegrini, N. Bouloufa, O. Dulieu, D. Comparat, P. Pillet, Sci. Agric. 321, 232 (2008).
D. Press, K.D. Greve, P.L. McMahon, T.D. Ladd, B. Friess, C. Schneider, M. Kamp, S. Höfling, A. Forchel, Y. Yamamoto, Nat. Photonics. 4, 367 (2010).
J. Hu, G. M. Vanacore, Z. Yang, X. Miao, A. H. Zewail. ACS Nano 9, 6728 (2015).
Kimel, A. V., A. Kirilyuk, P. A. Usachev, R. V. Pisarev, A. M. Balbashov, Th. Rasing. Nature 435, 7042 (2005).
Hu, J., Karam, T.E., Blake, G.A. and Zewail, A.H., Chem. Phys. Lett. 683, 258 (2017).
Kaplan, M., Yoo, B.K., Tang, J., Karam, T.E., Liao, B., Majumdar, D., Baltimore, D., Jensen, G.J. and Zewail, A.H. Angew. Chem. Int. Ed. 56, 11498 (2017).